Coordenadas polares
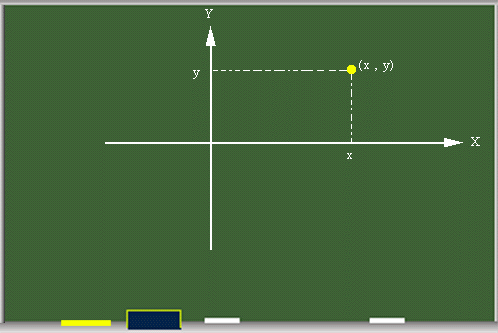
En un sistema de coordenadas rectangulares o cartesiano se puede localizar un punto con una sola pareja de puntos (x,y) estos valores son las distanicas dirigidas, partiendo del origen, desde los ejes x e y respectivamente. El origen es el punto donde se intersectan los dos ejes coordenados.
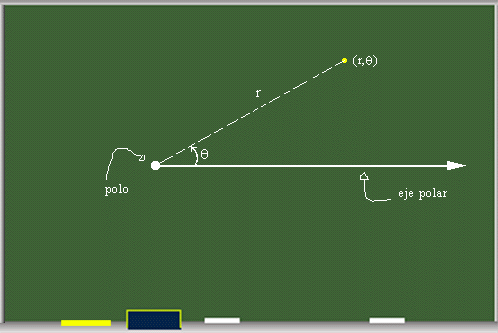
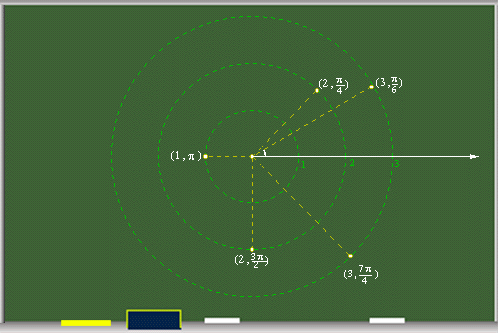
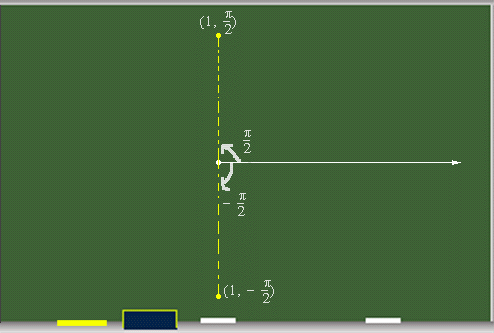
A continuación localizamos varios puntos en el plano polar.
 |  |
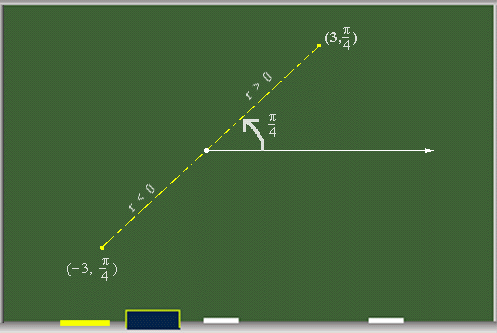
En este tipo de funciones la variable independiente es q y la dependiente es r, así que las funciones son del tipo r = r(q). El método para graficar estas funciones es el siguiente, primero graficamos la función r = r(q) en coordenadas rectangulares y apartir de esa gráfica trazamos la correspondiente en polares. Guiándonos con la dependencia de r con respecto a q.
Recordemos que q es la variable independiente y va de 0 a 2p generalmente. Por ejemplo la función r = q tiene como gráfica en rectangulares
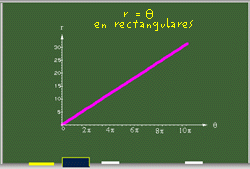 | A la izquierda vemos que el radio depende linealmente con el ángulo, es decir que el radio crecerá y tomará los mismos valores que el ángulo. Y a la derecha tenemos esta gráfica en coordenadas polares se ve claro esta dependencia del radio con el ángulo. A esta gráfica se le llama Espiral de Arquímedes | 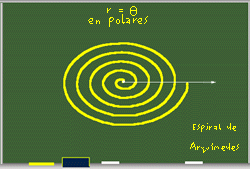 |
|  |
|  |
|  |
| 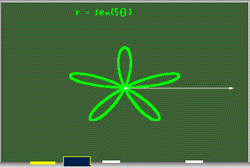 |
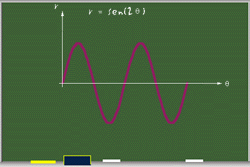
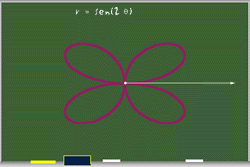
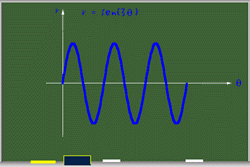
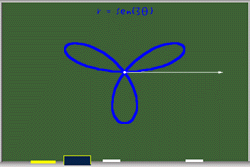
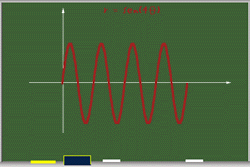
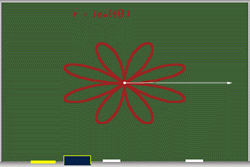
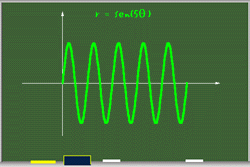
Hasta aqui hemos visto que las funciones del tipo r = sen(aq) son rosas o rosetas. El número de pétalos depende del valor de a, si a es par, el número de pétalos es 2a; y si a es impar el número de pétalos es a.
Para graficar estas funciones en el cuaderno o en el pizarrón se puede hacer una tabulación sólo con algunos valores de q que casi siempre son: 0, p/2, p, 3p/2, 2p. y ver cómo cambia el valor de r.
r = 1- sen(q)
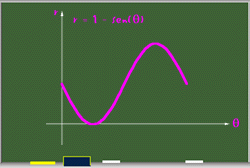
| Aquí observamos que el radio siempre es positivo y va de 1 a 2. | 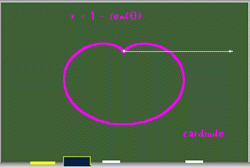 |
No hay comentarios.:
Publicar un comentario