Ecuación paramétrica

En matemáticas, una ecuación paramétrica permite representar una o varias curvas o superficies en el plano o en el espacio, mediante valores arbitrarios o mediante una constante, llamada parámetro, en lugar de mediante una variable independiente de cuyos valores se desprenden los de la variable dependiente. Un ejemplo simple de la cinemática, es cuando se usa un parámetro de tiempo para determinar la posición y la velocidad de un móvil.

Un ejemplo de una curva definida por ecuaciones paramétricas es la curva mariposa.

 

Descripción

En el uso estándar del sistema de coordenadas, una o dos variables (dependiendo de si se utilizan dos o tres dimensiones respectivamente) son consideradas como variables independientes, mientras que la restante es la variable dependiente, con el valor de ésta siendo equivalente al de la imagen de la función cuando los restantes valores son sus parámetros. Así por ejemplo la expresión de un punto cualquiera equivale a la expresión .
Esta representación tiene la limitación de requerir que la curva sea una función de x en y, es decir que todos los valores x tengan un valor y sólo un valor correspondiente en y. No todas las curvas cumplen con dicha condición. Para poder trabajar con la misma como si se tratara de una función, lo que se hace es elegir un dominio y una imagen diferentes, en donde la misma sí sea función. Para hacer esto, tanto x como y son considerados variables dependientes, cuyo resultado surge de una tercera variable (sin representación gráfica) conocida como «parámetro».

Ejemplo

Sea la ecuación general de una recta, entonces caben las ecuaciones paramétricas: , .¹

Otro ejemplo

Dada la ecuación , una parametrización tendrá la forma
Una parametrización posible sería
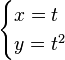
Se debe destacar que para cada curva existen infinitas parametrizaciones posibles. Una en donde x e y equivaliesen a y sería igualmente válida. La diferencia sería que, para encontrar un punto determinado (a, b) de la curva, el valor del parámetro sería diferente en cada caso. Con el ejemplo dado, el punto (2, 4) de la curva aparecería en la primera parametrización cuando t = 2, y en el segundo cuando U = 1.